بهینه ساز (optimizer)

یکی از مهم‌ترین تکنیک‌های که در یادگیری ماشین وجود دارد Optimizer ها هستند و نقش مهمی در حل مسائل پیچیده در زمینه‌های مختلف را ایفا می‌کنند، به خصوص در یادگیری عمیق. وظیفه اصلی این تکنیک کاهش تابع هزینه (Loss function) در طی فرآیند آموزش است. در این مقاله ما سعی می‌کنیم به طور کلی تعریف درستی از نحوه کار Optimizer ها داشته باشیم و در نهایت راه‌کار مناسبی برای انتخاب بهترین optimizer را ارائه کنیم.

الگوریتم بهینه سازی مدل چیست؟

همانطور که در مقاله شبکه عصبی کانولوشنی اشاره شد( می‌توانید این مقاله را در این لینک بخوانید) هر شبکه عصبی از چندین لایه مختلف تشکیل شده‌اند و درون هر لایه تعدادی نورون وجود دارد که هر کدام از آن‌ها تابع فعال سازی دارند که روی داده‌های که از لایه قبل گرفته‌اند محاسباتی را انجام می‌دهند و نتیجه را به لایه بعدی انتقال می‌دهند. ( شما می‌توانید مقاله مربوط به توابع فعال سازی و اهمیت آن‌ها را در این لینک بخوانید). 

قدرت اتصال بین هر نورون در لایه‌های مختلف توسط وزن‌ها و بایاس‌های آن تنظیم می‌شود ( نحوه اتصال هر نورون و قدرت اتصال هر لایه به لایه دیگر را در این لینک می‌توانید به صورت شماتیک ببینید). این پارامتر‌ها در طول فرایند آموزش به صورت مکرر تنظیم و به روز رسانی می‌شوند تا اختلاف بین خروجی مدل و خروجی مورد نظر به حداقل ممکن برسد. این اختلاف از طریق یک تابع که به عنوان تابع ضرر یا Loss function محاسبه می‌شود.

این تنظیمات توسط یک الگوریتم بهینه سازی کنترل می‌شود که با استفاده از گرادیان‌های که از طریق فرآیند پس‌انتشار خطا محاسبه می‌شوند، تعیین می‌کنند که وزن‌ها چگونه تغییر کنند تا میزان خطا کاهش پیدا کند. از آنجایی که تعداد پارامترها بسیار بزرگ و چند بعدی هستند، این الگوریتم‌های بهینه سازی باید به طور کارآمدی در این فضا حرکت کنند تا بتواند مجموعه وزن‌های بهینه برای مدل بدست آید.

برای رسیدن به این هدف لازم است که الگوریتم‌های بیهنه‌سازی یک تعادلی در بخش جستجو و همچنین Exploitation برقرار کند. بخش جستجو به مدل کمک‌ می‌کند که مسیرهای مختلفی برای پیدا کردن نقطه بهینه را امتحان کند، در طرف دیگر بخش Exploitation از اطلاعاتی که از گرادیان‌ها بدست آمده است برای حرکت سریع‌تر به سمت کاهش خطا استفاده می‌کند.

به طور کلی به این فرآیند انتشار خطا در مدل Backpropagation یا پس انتشار خطا گفته می‌شود.

Gradient Descent چیست؟

گرادیان نزولی یا همان (Gradient Descent) یک الگوریتم بهینه‌سازی است که برای کمینه‌سازی یک تابع استفاده می‌شود. این الگوریتم به‌صورت تکراری مقدار تابع را کاهش می‌دهد تا به حداقل مقدار آن برسد. ایده اصلی آن بر اساس محاسبه گرادیان (مشتق) تابع در یک نقطه خاص و حرکت در جهت منفی آن است، زیرا گرادیان نشان می‌دهد که تابع چگونه تغییر می‌کند و جهت نزولی‌ترین مسیر را مشخص می‌کند.

برای این که بتوانیم عملکرد این الگوریتم را بهتر درک کنیم از یک مثال استفاده می‌کنیم. فرض کنید که یک کوهنورد می‌خواهد به پایین‌ترین قسمت کوه حرکت کند، اما فقط می‌تواند شیب جای که در آن ایستاده است را حس کند. کوهنورد از یک نقطه تصادفی حرکت را آغاز می‌کند و فقط می‌تواند شیب زمین زیر پایش را حس کند. برای رسیدن به پایین‌ترین نقطه دره، او در جهت تندترین سراشیبی قدم برمی‌دارد. این تشبیه نشان می‌دهد که الگوریتم گرادیان نزولی نیز با استفاده از اطلاعات شیب تابع، قدم‌به‌قدم مقدار آن را کاهش می‌دهد تا به حداقل مقدار ممکن برسد.

اما همان‌طور که گفته شد محیط جستجو برای یک مدل چند بعدی است و به صورت شکل بالا ساده نیست، گاهی مقدار کمینه های مختلفی وجود دارد(کمینه‎های محلی) و باعث می‌شود که الگوریتم نتواند بهینه اصلی را پیدا کند، از طرف دیگر فضای جستجو چند بعدی است و باید نقطه مناسب پیدا شود.

امروزه همه الگوریتم‌های بهینه‌سازی‌ یادگیری عمیق از این گرادیان کاهشی برای یافتن بهترین وزن و به حداقل رساندن تابع هزینه استفاده می‌کنند. اگر بخواهیم یک تعریف ساده از تابع هزینه داشته باشیم می‌توانیم این گونه بگویم که: تابع هزینه برابر است با میانگین خطای محاسبه شده توسط loss function بر روی تمامی نمونه‌های آموزشی.

مراحل اجرای الگوریتم

در این قسمت مراحل اجرای الگوریتم را بررسی می‌کنیم.

در مرحله اول و شروع به کار الگوریتم تمامی وزن‌ها به صورت تصادفی مقدار دهی اولیه می‌شوند. 

در این مرحله گرادیان (مشتق) تابع هزینه نسبت به وزن هر نورون محاسبه می‌شود. گرادیان یک بردار جهت‌دار است که جهت بیشترین افزایش مقدار تابع را نشان می‌دهد، اما همانطور که گفت شد در اینجا ما به دنبال کمینه کردن تابع هزینه هستیم از این رو باید از گرادیان منفی استفاده کنیم تا مقدار بیشترین کاهش را پیدا کنیم.

در این مرحله وزن‌های مدل در جهت گرادیان منفی به‌روز رسانی می‌شود تا مقدار تابع هزینه کاهش پیدا کند، اما این تغییرات یکجا انجام نمی‌شود و با استفاده از learning rate یا نرخ یادگیری که تعیین می‌کند مدل با چه سرعتی در مسیر بهینه شدن حرکت کند انجام می‌گیرد. انتخاب درست مقدار نرخ یادگیری یکی از پارامترهای است که باید در فرایند یادگیری مدل تنظیم شود. اگر نرخ یادگیری بزرگ باشد ممکن است مدل به نوسان درآید و همگرا نشود و اگر خیلی کوچک باشد یادگیری مدل بسیار کند پیش خواهد رفت.

نمایش ریاضی 

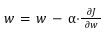
از رابطه بالا برای به روز رسانی وزن‌ها استفاده می‌شود که در آن:

وزن فعلی را با w نشان داده شده است.

نرخ یادگیری شبکه را با α نشان می‌دهد.

در نهایت گرادیان تابع هزینه نسبت به وزن w

این فرایند تا زمانی که تابع هزینه به حداقل مقدار ممکن خود برسد یا تغییرات آن بسیار ناچیز شود ادامه پیدا می‌کند.

چالش ها

در مسائل بهینه‌سازی پیچیده مانند یادگیری عمیق، تابع هزینه یک تابع خطی و ساده نیست بلکه چند بعدی و دارای پستی و بلندی‌های زیادی است که باعث می‌شود گرادیان نزولی در این نقاط گیر کنند. به زبان دیگر می‌توان گفت که در یادگیری عمیق توابع هزینه عملا غیر محدب (non-convex) هستند که دارای ویژگی‌های هستند که در این جا به مهم‌ترین آن‌ها اشاره میکنیم.

1. کمینه محلی (local Minimum): نقطه‌ای است که تابع هزینه مقدار کمی دارد اما ممکن است که کمترین مقدار ممکن در تابع هزینه نباشد.
2. نقطه زینی(Saddle Point): نقطه‌ای است که در برخی جهات ممکن است مقدار کمینه‌ باشد، اما در جهت دیگر مقدار بیشینه باشد. اگر گرادیان نزولی در این نوع از نقاط گیر کنند ممکن است که نتواند به سمت مقدار بهینه واقعی حرکت کند.
3. انتخاب نرخ یادگیری مناسب: همان‌طور که گفته شد نرخ یادگیری یک پارامتر است که باید برای محاسبه گرادیان نزولی مقدار مناسب آن تعیین شود. در صورتی که نرخ یادگیری زیاد باشد احتمال نوسان در روند یادگیری وجود دارد و مدل هیچ گاه همگرا نمی‌شود در مقابل اگر نرخ یادگیری کم باشد زمان یادگیری مدل افزایش پیدا می‌کند.

Stochastic Gradient Descent

گرادیان نزولی تصادفی یا به اختصار (SGD) یک الگوریتم اصلاح شده از گرادیان نزولی معمولی است که در آن فرآیند بهینه سازی به صورت تصادفی برای افزایش کارایی و سرعت همگرایی انجام می‌شود. مثال کوهنورد برای تعریف گرادیان نزولی را به خاطر بیاورید. در روش گرادیان نزولی معمولی، کوهنورد بسیار محتاط است به طوری که قبل از این که گامی بردارد تمامی محیط اطراف خود را تحلیل می‌کند تا شیب را به درستی و با دقت بالا محاسبه کند. این روش بسیار دقیق اما سرعت پایینی دارد. در طرف مقابل و در الگوریتم SGD، این کوهنورد فقط بر اساس شیب نقطه‌ای که در آن قرار دارد تصمیم می‌گیرد که به کدام سمت حرکت کند. اگر چه این کار باعث می‌شود که کوهنورد گام اشتباهی بردارد در عین حال سریعتر از روش قبلی حرکت می‌کند و می‌تواند از برخی از کمینه‌های محلی فرار کند.

به زبان دیگر می‌توان گفت که در SGD به جای این‌که بر روی کل مجموعه داده‌ها محاسبه شود، بر روی یک نمونه تصادفی در هر مرحله ارزیابی می‌شود که باعث افزایش سرعت در بهینه سازی می‌شود اما در مقابل نوسان بیشتری در مسیر یادگیری دارد.

مراحل انجام الگوریتم

در مرحله اول یک مقدار تصادفی برای تمامی وزن‌های شبکه در نظر گرفته می‌شود. در گام بعدی به جای این که گرادیان بر روی تمام مجموعه داده‌ها محاسبه شود بر روی یک نمونه تصادفی از روی داده‌های آموزش محاسبه می‌شود. در مرحله سوم مدل در جهت مخالف گرادیان حرکت می‌کند تا تابع هزینه را کاهش دهد. این فرآیند تا زمانی که تابع هزینه به کمترین میزان خود برسد یا تغییرات ناچیزی داشته باشد ادامه پیدا می‌کند.

نمایش ریاضی 

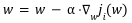
رابطه ریاضی بروزرسانی وزن‌ها در این الگوریتم به شکل بالا تعریف می‌شود که در آن:

• وزن‌های مدل با w نمایش داده شده است.
• نرخ یادگیری مدل با α نمایش داده شده است که عملا نشان می‌دهد تغییرات وزن چقدر بزرگ و یا کوچک باشد.
• تابع هزینه مربوط به نمونه i

چالش‌ها

از آن‌جایی که برای به روزرسانی وزن‌ها فقط از یک نمونه تصادفی استفاده می‌شود واریانس تابع هزینه بسیار زیاد است به عبارت دیگر تابع هزینه دارای نوسان زیادی است که ممکن است به جای همگرا شدن به یک مقدار ثابت، مقادیر تابع هزینه افزایش و یا کاهش شدیدی داشته باشد. از طرف دیگر میزان تغییرات به اندازه نرخ یادگیری (Learning rate) وابسته است و باید میزان دقیق آن با آزمایش به صورت دستی بدست آید.

مزایا 

بر خلاف گرادیان نزولی در حالت استاندارد به دلیل محاسبه بر روی یک نمونه تصادفی سرعت آن بسیار بیشتر است، همچنین نیاز به حافظه کمتری دارد و این موضوع در زمانی که داده‌های آموزش بزرگ و تعداد زیادی دارد بسیار مفید است. همان‌طور که پیشتر نیز گفته شد این الگوریتم دارای نوسان زیادی است که باعث می‌شود در تله کمینه‌های محلی گیر نکند و استفاده از آن در زمانی که تابع هزینه پیچیده و غیر محدب است بسیار مفید می‌باشد. از این الگوریتم برای سیستم‌های مانند سیستم‌های توصیه‌گر که جریان داده‌ها به صورت پیوسته به روز می‌شود و داده‌های جدید اضافه می‌شود مناسب است.

Mini-batch Gradient Descent

گرادیان نزولی مینی بچ یک روش ترکیبی برای رسیدن به تعادل بین گرادیان نزولی استاندارد و گرادیان نزولی تصادفی است. همانند الگوریتم‌های دیگر برای درک بهتر نحوه کار این الگوریتم از مثال کوهنورد استفاده می‌کنیم. 

در این روش به جای یک کوهنورد، گروهی از کوهنوردان را داریم که به صورت جداگانه مسیرهای مختلفی را مورد بررسی قرار می‌دهند، هر کدام از کوهنوردها بهترین مسیری که پیدا کرده است را با دیگر کوهنوردان به اشتراک میگذارد و به صورت گروهی بهترین مسیرها را مورد بررسی قرار می‌دهند تا از بین آن‌ها بهترین را انتخاب کنند. 

به عبارت دیگر در این روش به جای این که گرادیان کل داده‌ها محاسبه شود و یا این که گرادیان یک نمونه داده تصادفی مورد بررسی قرار گیرد، یک mini batch (گروه کوچکی از داده‌ها) انتخاب می‌شود و بر اساس آن گرادیان محاسبه می‌شود. این کار باعث افزایش سرعت نسبت به گرادیان کاهشی استاندارد و کاهش سرعت نسبت به SGD می‌شود.

مراحل انجام الگوریتم

در مرحله اول همانند دیگر الگوریتم‌ها یک مقدار تصادفی به تمام وزن‌ها اختصاص داده می‌شود تا فرآیند یادگیری شروع شود. در گام دوم که نیاز به محاسبه گرادیان است بر خلاف دو الگوریتم گذشته یه مجموعه‌ای از داده‌ها که به آن mini-batch  گفته می‌شود انتخاب و مقدار گرادیان آن محاسبه می‌شود. در گام سوم وزن‌های مدل در جهت مخالف گرادیان محاسبه شده و برای هر گروه mini-batch  تنظیم می‌شود. این الگوریتم سریعتر از گرادیان استاندارد است و نسبت به SGD ثبات بیشتری دارد.

نمایش ریاضی 

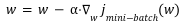
رابطه بروز رسانی وزن‌ها در این الگوریتم به صورت بالا تعریف می‌شود، همانطور که مشخص است این رابطه شبیه به رابطه گرادیان نزولی است با این تفاوت که از mini-batch  استفاده می‌شود. در رابطه بالا:

وزن ها را با w نمایش میدهیم.

نرخ یادگیری در این الگوریتم با α نمایش داده شده است.

تابع هزینه برای هر mini-batch

چالش‌ها

علاوه بر این‌ که نیاز است نرخ یادگیری درستی برای این الگوریتم انتخاب شود، باید سایز batch نیز به درستی انتخاب شود، در صورتی که سایز بزرگی برای دسته‌ها انتخاب شود الگوریتم رفتاری شبیه به گرادیان کاهشی استاندارد خواهد داشت و در صورتی که سایز دسته‌ها کم باشد رفتار الگوریتم شبیه به SGD خواهد بود. بنابر این پارامترهای که باید برای این الگوریتم با استفاده از سعی و خطا به دست آید بیشتر است.

مزایا

از مزایای این الگوریتم می‌توان به پایداری بیشتر آن نسبت به الگوریتم SGD اشاره کرد، همانطور که گفته شد انتخاب دسته‌ای از داده‌ها باعث می‌شود تغییرات گرادیان کاهش پیدا کند. از طرف دیگر نحوه عملکرد و وجود mini-batch باعث می‌شود که این الگوریتم را به صورت موازی بر روی پردازنده‌های گرافیکی (GPU) پیاده سازی کنیم. نکته مهم‎تری که در مورد این الگوریتم وجود دارد قابلیت تعمیم پذیری بالای آن به دلیل استفاده از mini-batch است که باعث می‌شود مدل کمتر دچار بیش برازش یا overfitting شود.

Adaptive Gradient Algorithm

این الگوریتم که به اختصار AdaGrad نامیده می‌شود نرخ یادگیری را به طور پویا تنظیم می‌کند. مثال کوهنوردان را به یاد بیاورید.حال فرض کنید که این کوهنوردان یک نقشه راه دارند که نشان می‌دهد در مسیر‌های سخت و پرشیب باید قدم‌های کوچک بردارند و در مسیر‌های راحت و هموار می‌توانند قدم‌های بزرگتری بردارند. بر خلاف الگوریتم‌های گذشته که یک نرخ یادگیری ثابت تعریف می‌شد در این الگوریتم نرخ یادگیری به صورت جداگانه برای هر پارامتر تنظیم می‌شود. در برخی از مدل‌ها بعضی از ویژگی‌ها ممکن است بسیار مهم باشند اما به ندرت در نمونه‌های آموزشی اتفاق بی‌افتند، این ویژگی AdaGrad باعث می‌شود که ضرایب مربوط به این ویژگی‌ها به درستی بهینه شود تا نقش درستی را در پیش‌بینی ایفا کند.

مراحل انجام الگوریتم 

پارامترهای مدل به صورت تصادفی مقدار دهی اولیه می‌شوند، در کنار این کار یه متغیر کمکی برای ذخیره سازی مجموع مربعات گرادیان‎ها نیز تعریف می‌شود. در گام بعدی همان‌طور که گرادیان هر پارامتر محاسبه می‌شود مقدار مربع گرادیان آن نیز در متغیر کمکی ذخیره و به مجموع قبلی اضافه می‌شود. در گام بعدی نرخ یادگیری هر پارامتر متناسب با ریشه دوم مجموع مربعات گرادیان کاهشی تنظیم می‎شود، به این صورت که اگر تغییرات زیاد باشد نرخ یادگیری کاهش پیدا می‌کند و اگر تغییرات کم باشد نرخ یادگیری افزایش پیدا می‌کند. در گام آخر نیز با استفاده از نرخ یادگیری جدید و مقدار گرادیان آن به روز رسانی می‌شود.

نمایش ریاضی

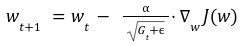
نحوه بروزرسانی وزن‌های شبکه از رابطه بالا بدست می‌آید که در آن:

وزن شبکه را با w نمایش داده‌ایم.

نرخ یادگیری اولیه را با α نمایش داده شده است.

مجموع مربعات گرادیان نیز با Gt نمایش داده شده است.

همچنین یک مقدار بسیار کم برای جلوگیری از تقسیم بر صفر شدن کسر که ϵ نشان داده شده است در مخرج کسر قرار می‌گیرد.

گرادیان تابع هزینه نسبت به پارامترها در زمان t

چالش‌ها

یکی از مهمترین چالش‌‌های این الگوریتم کاهش بیش از حد نرخ یادگیری در طول فرآیند آموزش است زیرا مجموع مربعات گرادیان در طول زمان افزایش پیدا می‌کندو زمانی که Gt خیلی بزرگ شود، مقدار کسر αGt​+ϵ خیلی کوچک می‌شود و باعث می‌شود که مدل نتواند وزن‌ها را به درستی به روز رسانی کند.

مزایا

مهمترین مزیت استفاده از این الگوریتم نرخ یادگیری تطبیقی است که برای هر پارامتر به صورت اختصاصی تنظیم می‌شود. این مزیت باعث می‌شود که این الگوریتم برای داده‌ها با ویژگی‌های پراکنده (Sparse Features) مفید باشد. از طرف دیگر این الگوریتم ساده و کارایی زیادی دارد و نیاز به تنظیم دستی نرخ یادگیری را از بین می‌برد.

Root Mean Square Propagation

الگوریتم بهینه‌سازی که به اختصار RMSprop نامیده می‌شود یک الگوریتم بهینه‎سازی با نرخ یادگیری تطبیقی است که از روی AdaGrad طراحی شده است اما سعی می‌کند راه‌حلی برای توقف یادگیری در زمانی که نرخ یادگیری به مرور زمان کم شده است داشته باشد. برای حل این مشکل به جای مجموع مربعات گرادیان، یک میانگین متحرک نمایی از آن را نگه می‌دارد. این کار باعث می‌شود که نرخ یادگیری در یک محدوده معقول بماند.

دوباره مثال کوهنوردان را به یاد بیاورید، در الگوریتم قبلی کوهنوردان پس از مدتی گام‌های کوچکتری بر می‌دارند تا زمانی که به طور کامل متوقف می‌شوند. حال فرض کنید که کوهنوردان یک ابزار هوشمندی دارند که بر اساس شرایط اخیر مسیر اندازه گام‌هایشان را تنظیم می‌کنند در این حالت بدون این که در مسیرهای دشوار گیر کنند می‌توانند به مقصد برسد. 

مانند دیگر الگوریتم‌ها هدف اصلی این الگوریتم پیدا کردن مقدارهای بهینه وزن‌ها است به طوری که تابع هزینه به حداقل خود برسد. برخلاف الگوریتم AdaGrad این الگوریتم از یک میانگین متحرک استفاده می‌کند تا از کوچک شدن بیش از حد نرخ یادگیری جلوگیری کند.

مراحل انجام الگوریتم

در گام نخست مانند دیگر الگوریتم‌ها یک مقدار دهی اولیه برای تمامی وزن‌ها انجام می‌شود، همچنین یک میانگین متحرک نمایی از مربعات گرادیان‌ها تعریف می‌شود که در مرحله اول صفر است. در گام بعدی گرادیان تابع هزینه برای هر پارامتر محاسبه می‌شود، معمولا برای محاسبه گرادیان از mini-batch انجام می‌شود. در گام بعدی ما نیاز داریم که میانگین متحرک گرادیان را به روز رسانی کنیم، برای این‌کار ما یک عامل کاهش به نام گاما( γ ) در نظر می‌گیریم، این متغیر برای تنظیم اهمیت گرادیان‌های قبلی استفاده می‌شود، این کار باعث می‌شود که گرادیان‌های اخیر وزن بیشتری داشته باشند و گرادیان مراحل قبل‌تر تاثیر کمتری بگذارند. 

نمایش ریاضی

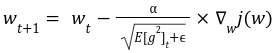
رابطه به‌روز رسانی وزن‌های شبکه در این الگوریتم به صورت رابطه بالا تعریف شده است که در آن:

وزن‌ها را با w نمایش داده‌اند.

نرخ یادگیری الگوریتم α است.

میانگین متحرک مربعات گرادیان در لحظه t

همانطور که گفته شد این مقدار یک میانگین متحرک نمایی از مربعات گرادیان است که با یک ضریب کاهشی تدریجی به روز می‌شود و از رابطه زیر به دست می‌آید.

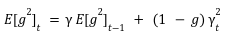
این مقدار باعث می‌شود که مقدار گرادیان‌های اخیر وزن بیشتری داشته باشند و از نوسانات شدید پارامترها جلوگیری کنند.

مزایا

در روش‌های ساده‌تر مثل گرادیان نزولی معمولی ما یک نرخ یادگیری ثابت برای همه پارامتر‌ها در نظر گرفته بودیم که باعث می‌شد یادگیری یا بسیار کند و یا بسیار سریع شود. اما در این الگوریتم یادگیری به صورت تطبیقی اتفاق می‌افتد به این معنی که نرخ یادگیری بر اساس مقادیر اخیر هر گرادیان تغییر می‌کند. این ویژگی الگوریتم باعث می‌شود که برای داده‌های با ویژگی‌های نادر بسیار مناسب باشد.

در الگوریتم AdaGrad که قبلا بررسی کردیم، گرادیان‌های به دست آمده همواره با یکدیگر جمع می‌شدند و مدام در حال افزایش بودند و این امر باعث می‌شد که نرخ یادگیری همیشه در حال کاهش باشد و در نهایت باعث می‌شد که یادگیری الگوریتم متوقف شود. اما از آنجایی که در الگوریتم RMSprop روی گرادیان‌های اخیر تمرکز دارد و از میانگین متحرک نمایی استفاده می‌شود باعث می‌شود که یادگیری به طور مداوم اتفاق بی‌افتد.

AdaDelta

این الگوریتم نسخه بهبود یافته‌ای از الگوریتم AdaGrad است که می‌خواهد مشکل کاهش بیش‌از حد نرخ یادگیری را حل کند. برای درک بهتر این الگوریتم دوباره به سراغ مثال کوه‌نوردان می‌رویم، در این روش دوباره فرض کنید که کوهنوردان یک وسیله هوشمندی دارند که فقط مسیر‌های که اخیرا از آن استفاده کردند را در نظر می‌گیرند و مسیر‌های قدیمی‌تر را حذف می‌کنند. این کار باعث می‌‌شود که سرعت پیش‌روی آن‌ها همچنان بالا باشد. 

تفاوت اصلی این الگوریتم با AdaGrad وجود یک پنجره متحرک است که گرادیان‌های اخیر را در نظر می‌گیرد بنابراین نرخ یادگیری به طور ناگهانی صفر نمی‌شود و مدل همچنان می‌تواند یاد بگیرد.

هدف اصلی در این الگوریتم استفاده از نرخ یادگیری به‌صورت تطبیقی بدون نیاز به مقداردهی اولیه است از طرف دیگر برخلاف RMSprop، این الگوریتم مستقیما نسبت به تغییرات را به جای نرخ یادگیری به عنوان فاکتور تنظیم کننده استفاده می‌شود.

مراحل انجام الگوریتم

در مرحله اول دو متغیر به نام Accumulated Gradients برای نگهداری مجموع مربعات گرادیان‌ها و دیگری Accumulated Updates باری ذخیره‌سازی مجموع مربعات تغییرات وزن‌ها تعریف می‌شود که در مرحله اول مقدار صفر است. در گام دوم گرادیان تابع هزینه نسبت به هر پارامتر محاسبه می‌شود، همچنان برای این محاسبه از mini-batch استفاده می‌شود. در گام سوم مقدار متغیر مربعات گرادیان‌ها به‎روزرسانی می‌شود، برای این‌کار از یک فاکتور کاهشی استفاده می‌شود که گرادیان‌های جدید وزن بیشتری بگیرند. در مرحله بعدی پارامترهای شبکه با استفاده از نسبت جذر مجموع مربعات تغییرات قبلی به جذر مجموع مربعات گرادیان‌ها محاسبه می‌شود. این روش باعث حذف نرخ یادگیری می‌شود و مستقیما اندازه تغییرات را متناسب با تغییرات گذشته مقیاس‌بندی می‌کنند. یک مقدار اپسیلون نیز به مخرج کسر اضافه می‌شود تا از صفر شدن آن جلوگیری شود. 

این الگوریتم برخلاف AdaGrad که نرخ یادگیری به مرور کاهش پیدا می‌کند، مقدار به‌روزرسانی‌ها متناسب با تغییرات اخیر تنظیم‌ می‌کند. از طرف دیگر برخلاف RMSprop که یک مقدار نرخ یادگیری اولیه نیاز دارد، این الگوریتم نیازی به نرخ یادگیری اولیه ندارد.

نمایش ریاضی

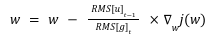
رابطه به‎‌روزرسانی الگوریتم یه شکل بالا تعریف شده است که در آن:

میانگین متحرک نمایی از مربعات گرادیان تا زمان t را با RMS[g] نمایش می‎دهند.

میانگین متحرک نمایی از مربعات تغییرات پارامترها تا زمان t-1 را با RMS[u] نمایش می‌دهند.

همان‌طور که معلوم است در این الگوریتم دیگر نرخ یادگیری نداریم و یادگیری بر اساس تغییرات قبلی خود تنظیم می‌شود. از طرف دیگر به دلیل میانگین متحرک نمایی، تاثیر گرادیان‌های قبلی کم می‌شود. 

چالش‌ها

برخلاف روش‌های قبلی که فقط به نرخ یادگیری نیاز است در این روش دو متغییر میانگین متحرک نمایی و به‌روزرسانی مورد نیاز است و باید در حافظه نگهداری شود. این موضوع پیاده سازی الگوریتم را پیچیده‌تر می‌کند. از طرف دیگر این الگوریتم نسبت به روش‌های دیگر دیرتر همگرا می‌شود. این مشکل به دلیل مکانیسم تنظیم‌ نرخ یادگیری است. 

مزایا

یکی از بزرگترین مزایای این الگوریتم نرخ یادگیری خود تنظیم شونده است، با این روش دیگر نیازی نیست که یک مقدار اولیه به عنوان نرخ یادگیری تنظیم شود. استفاده از یک پنجره محدود از مقادیر گذشته باعث می‌شود که نرخ یادگیری به یک باره کاهش پیدا نکند و مقدار محدودی از گرادیان‌های اخیر در نظر گرفته شود.

Adaptive Moment Estimation

این الگوریتم که به اختصار به نام Adam تعریف می‌شود یک ترکیب از بهترین ویژگی‌های AdaGrad و  RMSprop است و یک الگوریتم پیشرفته بهینه‌سازی محسوب می‌شود.

هدف اصلی این الگوریتم استفاده از نرخ یادگیری تطبیقی و کنترل جهت حرکت است تا مسیر را زودتر بهینه کند. مثال کوهنوردان را به یاد بیاورید، حال فرض کنید دستگاه پیشرفته‌ای به کوهنوردان داده شده است که علاوه بر سختی مسیر می‌تواند جهت حرکت را هم برای آن‌ها تنظیم کند. این ابزار از دو ویژگی مهم دستگاه‎های گذشته یعنی بررسی سرعت و جهت حرکت( مشابه RMSprop) و نگه‌داشتن حافظه‌ای از مسیر‌های قبلی برای تصحیح مسیر(مشابه AdaGrad) استفاده می‌کند. در نتیجه مسیر حرکت بهینه‌تر، یکنواخت‌تر و بدون انحراف‌های ناگهانی است.

در این روش گرادیان‌های قبلی ذخیره می‌شود و از آن‌ها برای هدایت و به‌روزرسانی استفاده می‌شود، همچنین از Moment Estimation برای کنترل اندازه و جهت به‌روزرسانی نیز استفاده می‌شود.

مراحل انجام الگوریتم

همانند تمامی الگوریتم‌های دیگر یک مقدار تصادفی برای پارامترها در نظر گرفته می‌شود، همچنین دو بردار Moment نیز مقداردهی اولیه می‌شود.

بردار اول که با m مشخص می‌شود برای میانگین گرادیان‌ها و بردار دوم که میانگین مربع گرادیان‌ها را ذخیره می‌کند و با v نمایش داده می‌شود. مقدار اولیه این بردارها صفر است. از آنجایی که دو بردار در لحظه اول صفر هستند مقدار به‌روزرسانی به سمت صفر میل می‌کند که برای رفع این مشکل از مکانیسم تصحیح بایاس استفاده می‌شود تا تاثیر مقدار اولیه صفر کاهش پیدا کند. در لحظه اول این مقدار عدد بزرگی است اما به مرور زمان به سمت یک نزدیک می‌شود.

در گام دوم گرادیان‌ها بر اساس mini-batch محاسبه می‌شوند و بعد از آن بردارهای Moments به‌روز رسانی می‌شوند. بردار m مقدار قبلی خودش را با مقدار جدید گرادیان ترکیب می‌کند تا جهت به‌روزرسانی را مشخص کند و بردار v مقدار قبلی خودش را با مربع گرادیان‌ها ترکیب می‌کند تا اندازه به‌روزرسانی را تنظیم کند. بردار m باعث می‌شود که مدل مسیر یادگیری را هموارتر دنبال کند و بردار v از بزرگ شدن مقادیر گرادیان جلوگیری می‎کند که باعث پایداری بیشتر یادگیری می‌شود.

در گام بعدی از مقادیر دو بردار استفاده می‌شود تا نرخ یادگیری برای هر پارامتر بهینه شود. با استفاده از این روش پارامترهای که گرادیان بزرگتری دارند به‌روزرسانی کوچکتری دریافت می‌کنند و بالعکس.

نمایش ریاضی

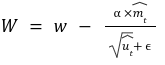
رابطه بالا نحوه به‌روزرسانی پارامترهای مدل را نشان می‎دهد که در آن:

میانگین متحرک گرادیان‌ها را باmt نمایش داده‌اند.

میانگین متحرک مربع گرادین‌ها را نیز با u نمایش داده شده است.

همان‌طور که گفته شد میانگین گرادیان‌ها را به عنوان m ذخیره می‌کنیم تا تغییرات ناگهانی کاهش پیدا کند و همچنین u را به عنوان میانگین مربعات گرادیان‌ها ذخیره می‌کنیم تا پارامترهای مختلف تنظیم شود.

مزایا

از مزایای این الگوریتم می‌شود به نرخ یادگیری تطبیقی اشاره کرد که بر اساس دو مقدار Moment  انجام می‌شود. مزیت استفاده از این روش پایداری بیشتر و بهینه‌سازی بهتر است. همچنین در ابتدا به دلیل صفر بودن مقادیر Moment میزان تخمین‌های اولیه به‌طور مصنوعی کوچک است که برای اصطلاح این کار از بایاس استفاده می‌شود تا شروع قوی‎تری داشته باشد و از کاهش سرعت یادگیری جلوگیری کند.

همچنین این الگوریتم از نظر محاسبانی مقرون‌به‌صرفه تر است و تنها نیاز به دو بردار اضافه دارد. این الگوریتم بر روی داده‌های بسیار بزرگ و شبکه‌های عصبی عمیق بسیار کاربردی تر است.

 انتخاب الگوریتم بهینه‌سازی برای مدل

در جدول زیر می‌توان یک مقایسه کلی بین تمام الگوریتم‌های بهینه‌ساز ها را دید و بر اساس مزایا و معایب آن‌ها بهترین آن‌ها را انتخاب کرد.

مناسب برای	معایب	مزایا	الگوریتم
داده‌های کوچک، زمانی که سادگی و شفافیت مهم است	محاسبات سنگین روی داده‌های بزرگ، امکان گیر کردن در کمینه‌های محلی	ساده و قابل درک	Gradient Descent
داده‌های بزرگ، یادگیری آنلاین یا تدریجی	نوسانات زیاد در گرادیان‌ها می‌تواند باعث بی‌ثباتی شود	سریع، مناسب برای داده‌های حجیم	SGD (گرادیان نزولی تصادفی)
اغلب مسائل یادگیری عمیق، داده‌های متوسط تا بزرگ	نیاز به تنظیم اندازه mini-batch	تعادل بین سرعت و پایداری، بروزرسانی‌های پایدارتر	Mini-batch Gradient Descent
داده‌های پراکنده مثل پردازش متن و تصاویر	نرخ یادگیری به صفر میل می‌کند و یادگیری متوقف می‌شود	نرخ یادگیری تطبیقی برای هر پارامتر، مناسب برای داده‌های پراکنده	AdaGrad
مسائل غیر محدب زمانی که AdaGrad خیلی سریع نرخ یادگیری را کاهش می‌دهد	ممکن است در کمینه‌های محلی گیر کند	حل مشکل کاهش شدید نرخ یادگیری در AdaGrad، نرخ یادگیری تطبیقی براساس گرادیان‌های اخیر	RMSprop
مشابه RMSprop، اما بدون نیاز به تنظیم دستی نرخ یادگیری	پیچیده‌تر از RMSprop و AdaGrad	نیازی به تعیین نرخ یادگیری اولیه ندارد، حل مشکل کاهش بیش از حد نرخ یادگیری	AdaDelta
اغلب مسائل یادگیری عمیق، بهینه‌سازی کار	نیاز به تنظیم ابرپارامترها (اما مقدار پیشفرض معمولا خوب کار می‌کند)	ترکیب مزایای AdaGrad و RMSprop، نرخ یادگیری تطبیقی، تصحیح بایاس	Adam

در این لینک می‌توانید الگوریتم‌های که توسط کتابخانه‌ keras پیاده سازی شده است را ببینید و در مدل خود استفاده کنید.