توابع فعال سازی

همانطور که در مقاله شبکه‌های عصبی پرسپترون چند لایه (می‌توانید مقاله را در این لینک بخوانید) بیان شد هر نورون دارای یک تابع فعال سازی است که باعث می‌شود که نورون‌ها توانایی استخراج الگوهای پیچیده‌تر را داشته باشند و سیگنال ورودی را بعد از پردازش به لایه بعدی انتقال می‌دهد. بدون استفاده از توابع فعال سازی شبکه‌ها فقط توانایی استخراج الگوهای خطی را از بین داده‌ها و ارتباط بین ورودی و خروجی را دارد. به زبان علمی‌تر می‌توان گفت که توابع فعال سازی غیر خطی این قابلیت را فراهم می‌کند که نگاشت‌های پیچیده بین ورودی و خروجی را درک کند. دانستن نحوه عملکرد توابع فعال سازی باعث می‌شود که شما بتوانید مدل‌های بهتر با دقت بالاتری داشته باشید.

انواع توابع فعال سازی 

انواع مختلفی از توابع فعال سازی در شبکه‌های عصبی مصنوعی وجود دارد این توابع عموما غیرخطی هستند و امکان یادگیری الگوهای پیچیده را برای شبکه‌های عصبی فراهم می‌کند.

Linear activation

یکی از ساده‌ترین توابع فعال سازی، تابع خطی است که به صورت f(x)=x تعریف می‌شود و به طور ساده هر چه در ورودی باشد به خروجی انتقال می‌دهد. از این تابع بیشتر در لایه‌های خروجی و زمانی که می‌خواهیم regression داشته باشیم و یک مقدار عددی را پیش‌بینی کنیم مورد استفاده قرار می‌گیرد، زیرا بدون هیچ تغییری مقدار ورودی خود را به خروجی خود منتقل می‌کند در این حالت مقدار واقعی پیش بینی به خروجی منتقل می‌شود. از آنجایی که این تابع توانایی استخراج ویژگی‌های غیر خطی را ندارد معمولا در لایه‌های پنهان شبکه‌های عصبی مورد استفاده قرار نمی‌گیرد.

Sigmoid activation

تابع فعال سازی سیگموید که معمولا با نماد (x) نمایش داده می‌شود، یک تابع صاف و پیوسته است که از نظر تاریخی نیز در شبکه‌های عصبی اهمیت زیادی دارد زیرا جزو اولین توابع‌ای بود که در شبکه‌های عصبی پیاده سازی شد.

رابطه تابع سیگموید به صورت زیر تعریف می‌شود:

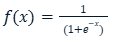
این تابع یک مقدار واقعی را به عنوان ورودی دریافت می‌کند و یه یک مقدار بین 0 تا 1 تبدیل می‌کند. همانطور که از شکل این تابع مشخص است یک منحنی به شکل S است که برای اعداد منفی خیلی بزرگ به سمت صفر میل می‌کند و برای اعداد مثبت خیلی بزرگ به سمت یک میل می‌کند. از این رو برای طبقه‌بندی دو کلاسه می‌تواند مفید باشد. این تابع در ابتدا در شبکه‌های عصبی بسیار محبوب بودند زیرا زمانی که خروجی این رابطه نزدیک به 0.5 باشد گردایان قوی‌تری دارد و امکان آموزش پس انتظار خطا نیز کارآمد تر خواهد بود اما زمانی که شبکه‌های عصبی عمیق شدند و تعداد لایه‌ها بیشتر شد مشکل vanishing gradient به وجود آمد.

زمانی که مقادیر ورودی نورون‌ها به طور قابل توجهی مثبت یا منفی است، خروجی تابع به سمت صفر و یک با شیب بسیار کم اشباع می‌شود و گرادیان به سمت صفر نزدیک می‌شود، این عمل باعث می‌شود که وزن‌های شبکه به خصوص در لایه‌های ابتدایی در زمان پس انتشار خطا تغییرات بسیار کم و ناچیزی داشته باشند یا در بعضی از موارد به طور کامل متوقف شوند. این مشکل را ناپید شدن گرادیان و یا vanishing gradient می‌گویند.

امروزه بیشتر از این تابع در لایه آخر برای دسته بندی‌های دو کلاسه استفاده می‌شود. 

Tanh (hyperbolic tangent) activation

تابع فعال سازی Tanh  که به صورت زیر تعریف می‌شود:

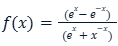
تابعی است که خروجی آن همان‌طور که در شکل مشخص است بین 1 و1- است و در این تابع تاثیر مقادیر منفی بیشتر بر روی خروجی مشخص می‌شود تا تابع سیگموید، همچنین شیب خط در این تابع بیشتر است که باعث می‌شود یادگیری سریعتر و همگرایی بهتر انجام شود، اما همچنان با مشکل ناپدید شدن گرادیان روبه رو است زیرا همانند تابع سیگموید ممکن است در طول فرایند پس انتشار خطا، گرادیان به مقدار زیادی کاهش پیدا کند و به سمت صفر میل کند و باعث می‌شود که عمل آموزش و به روزرسانی وزن‌ها به درستی انجام نشود.

از این تابع در لایه‌های پنهان شبکه بیشتر استفاده می‌شود زمانی که داده‌ها نرمال شده‌اند تا میانگین صفر داشته باشند استفاده از این تابع باعث آموزش کارآمدتر آن می‌شود.

ReLU (rectified linear unit) activation

تابع فعال سازی ReLU که با رابطه زیر تعریف می‌شود:

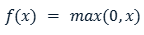
همانطور که مشخص است این تابع برای مقادیر منفی خروجی صفر را تولید می‌کند و در در مقادیر مثبت ورودی را به خروجی منتقل می‌کند و این موضوع باعث می‌شود که گرادیان بدون تغییر در طول فرآیند پس انتشار خطا به لایه‌های ابتدای منتقل شود و دیگر مشکل ناپدید شدن گرادیان به وجود نیاید. اگرچه این تابع برای بخشی از ورودی‌های خود خطی است، اما از نظر فنی یک تابع غیر خطی به شمار می‌آید.( زیرا در نقطه x=0 به طور ناگهانی خروجی تغییر می‌کند.) این غیر خطی بودن تابع همانند توابع دیگر غیر خطی باعث می‌شود که الگوهای پیچیده را بهتر یاد بگیرد.

از طرف دیگر تا زمانی که مقادیر منفی به این تابع ارسال شود خروجی صفر خواهد بود و این موضوع باعث می‌شود که نورون‌ها به طور پراکنده فعال شوند و این امر باعث محاسبه کارآمدتر می‌شود و همچنین از نظر بار محاسباتی نسبت به توابع دیگر کم هزینه‌تر بوده و به شبکه این اجازه را می‌دهد که بدون اضافه شدن بار محاسباتی خیلی زیاد از لایه‌های بیشتری استفاده کند.

Softmax activation

تابع فعال سازی Softmax که به عنوان تابع نمایی نرمال شده نیز شناخته می‌شود، بیشتر در موارد طبقه‌بندی چندکلاسه و در لایه آخر مورد استفاده قرار می‌گیرد. نحوه عملکرد این تابع به این شکل است که معمولا بر روی یک بردارد که نشان دهنده پیش‌بینی و یا امتیاز خام برای هر کلاس است که به آن logits گفته می‌شود عمل می‌کند. تابع softmax بر روی یک بردار که از المان‌های x1,x2,…,xn به صورت زیر تعریف می‌شود:

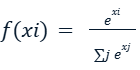
خروجی این تابع یک تابع توزیع احتمال است که مجموع آن برابر با یک است و هر عنصر خروجی در آن نشان دهنده احتمال تعلق ورودی به یک کلاس خاص است. استفاده از این تابع این اجازه را می‌دهد که ما مطمئن باشیم همواره خروجی این تابع غیر منفی باشد و این موضوع بسیار مهمی است زیرا که احتمالات نمی‌تواند منفی باشد.

در واقع می‌توان گفت که تابع، تفاوت‌های بردار ورودی را تقویت می‌کند به طوری که تفاوت‌های کوچک در ورودی باعث ایجاد تفاوت‌های بزرگ در خروجی می‌شود. 

در این مقاله سعی شد بخشی از توابع فعال سازی که بیشتر در شبکه‌ها استفاده می‌شود، توضیح داده شود(شما می‎توانید انواع توابعی که توسط کتابخانه keras پیاده سازی شده است را در این لینک مشاهده کنید). انتخاب نوع تابع فعال سازی برای شبکه یک کار بسیار مهم است به طوری که اگر تابع فعال سازی مناسبی برای شبکه انتخاب نشود، احتمال این که به جواب درستی در خروجی شبکه بدست نیاید وجود دارد.